foolish fly fox's blog

--Stay hungry, stay foolish.
--Forever young, forever weep.


博客主页为：https://foolishflyfox.github.io/CsLearnNote/

62. Unique Paths

https://leetcode.com/problems/unique-paths/description/

Description

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?


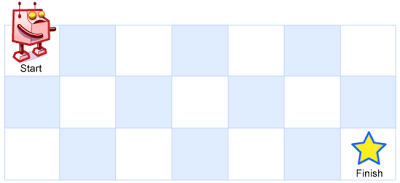
Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

  1. Right -> Right -> Down
  2. Right -> Down -> Right
  3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

Solution

class Solution:
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        route_num = dict()
        def get_paths(w, h):
            map_size = (min(w,h), max(w,h))
            if w==1 or h==1:
                return 1
            if map_size in route_num:
                return route_num[map_size]
            p1 = get_paths(w-1, h)
            p2 = get_paths(w, h-1)
            route_num[map_size] = p1+p2
            return p1+p2
        return get_paths(m, n)
≡