遗传算法计算旅行商问题

如下表所示，为一组中国城市的经纬度信息，现在要求从北京出发，旅行一圈，最后回到北京。这个过程中，同一个城市不能经过两次，两个城市之间的距离计算直接用经纬度作为坐标，求两者的欧拉距离即可：

编号	城市名	东经	北纬	编号	城市名	东经	北纬
1	北京	116.46	39.92	18	南京	118.78	32.04
2	天津	117.2	39.13	19	合肥	117.27	31.86
3	上海	121.48	31.22	20	杭州	120.19	30.26
4	重庆	106.54	29.59	21	福州	119.3	26.08
5	拉萨	91.11	29.97	22	南昌	115.89	28.68
6	乌鲁木齐	87.68	43.77	23	长沙	113	28.21
7	银川	106.27	38.47	24	武汉	114.31	30.52
8	呼和浩特	111.65	40.82	25	广州	113.23	23.16
9	南宁	108.33	22.84	26	台北	121.5	25.05
10	哈尔滨	126.63	45.75	27	海口	110.35	20.02
11	长春	125.35	43.88	28	兰州	103.73	36.03
12	沈阳	123.38	41.8	29	西安	108.95	34.27
13	石家庄	114.48	38.03	30	成都	104.06	30.67
14	太原	112.53	37.87	31	贵阳	106.71	26.57
15	西宁	101.74	36.56	32	昆明	102.73	25.04
16	济南	117	36.65	33	香港	114.1	22.2
17	郑州	113.6	34.76	34	澳门	113.33	22.13

暴力枚举

cities = [(116.46, 39.92),(117.2, 39.13),(121.48, 31.22),(106.54, 29.59),
          (91.11, 29.97),(87.68, 43.77),(106.27, 38.47),(111.65, 40.82),
          (108.33, 22.84),(126.63, 45.75),(125.35, 43.88),(123.38, 41.8),
          (114.48, 38.03),(112.53, 37.87),(101.74, 36.56),(117.0, 36.65),
          (113.6, 34.76),(118.78,32.04),(117.27,31.86),(120.19,30.26),
          (119.3,26.08),(115.89,28.68),(113.0,28.21),(114.31,30.52),
          (113.23,23.16),(121.5,25.05),(110.35,20.02),(103.73,36.03),
          (108.95,34.27),(104.06,30.67),(106.71,26.57),(102.73,25.04),
          (114.1,22.2),(113.33,22.13)]

from itertools import permutations
import math

# 使用枚举方式计算路径
def enum_TSP(cities):
    paths = permutations(range(1, len(cities)), len(cities)-1)
    shortest_path = None
    shortest_miles = None
    for path in paths:
        cur_miles = 0
        path = [0] + list(path)
        pre_pos = cities[path[-1]]
        for i in path:
            cur_miles += math.hypot(pre_pos[0]-cities[i][0],
                                   pre_pos[1]-cities[i][1])
            pre_pos = cities[i]
        if shortest_miles==None or shortest_miles>cur_miles:
            shortest_miles = cur_miles
            shortest_path = path
    return shortest_miles, shortest_path
import time
pre_running = 100000
# 测试随着城市个数的增加，计算时间的变化
for i in range(1,13):
    t1 = time.time()
    miles, path = enum_TSP(cities[:i])
    t2 = time.time()
    print("running:{:g}s x{:.3f}, miles:{}".format(
        t2-t1, (t2-t1)/pre_running, miles))
    pre_running = t2-t1

print(path)

测试结果为：

01 CITY # running:3.60012e-05s x0.000, miles:0.0
02 CITY # running:1.09673e-05s x0.305, miles:2.164901845350049
03 CITY # running:8.82149e-06s x0.804, miles:20.120564493919822
04 CITY # running:2.21729e-05s x2.514, miles:39.42664606580856
05 CITY # running:4.91142e-05s x2.215, miles:67.77227033726385
06 CITY # running:0.000365973s x7.451, miles:83.7957265568911
07 CITY # running:0.00200295s x5.473, miles:84.38275768767652
08 CITY # running:0.0180061s x8.990, miles:84.85443680089674
09 CITY # running:0.14526s x8.067, miles:92.40225788702355
10 CITY # running:1.16235s x8.002, miles:110.34594071307717
11 CITY # running:12.7086s x10.934, miles:110.43467064772815
12 CITY # running:148.912s x11.717, miles:110.6873206900153

[0, 1, 11, 10, 9, 2, 8, 3, 4, 5, 6, 7]

可以看出，随着节点个数的增加，时间复杂度不仅仅是以指数方式增大，而是以阶乘的方式增大。其中在有 12 个节点的时候用时就达到了149 s。

爬山法解TSP问题

from itertools import combinations
def climb_TSP(cities):
    shortest_path = [0] + random.sample(range(1, len(cities)),
                                        len(cities)-1)
    shortest_miles = None
    while True:
        swap_poses = combinations(range(1, len(cities)), 2)
        for p1, p2 in swap_poses:
            tp_path = shortest_path[:]
            tp_path[p1],tp_path[p2]=tp_path[p2],tp_path[p1]
            tp_miles = 0
            pre_pos = cities[tp_path[-1]]
            for p in tp_path:
                tp_miles += math.hypot(pre_pos[0]-cities[p][0],
                                      pre_pos[1]-cities[p][1])
                pre_pos = cities[p]
            if shortest_miles == None or shortest_miles>tp_miles:
                shortest_path = tp_path
                shortest_miles = tp_miles
                break
        else:
            break
    return shortest_miles, shortest_path

pre_running = 100000
for i in range(1,len(cities)):
    t1 = time.time()
    miles2, path2 = climb_TSP(cities[:i])
    t2 = time.time()
    print("running:{:g}s x{:.3f}, miles:{}".format(
        t2-t1, (t2-t1)/pre_running, miles2))
    pre_running = t2-t1
    
print(path2)

结果为：

01 CITY # running:2.09808e-05s x0.000, miles:None
02 CITY # running:1.78814e-05s x0.852, miles:None
03 CITY # running:0.0017221s x96.307, miles:20.120564493919822
04 CITY # running:6.48499e-05s x0.038, miles:39.42664606580856
05 CITY # running:0.000110865s x1.710, miles:67.77227033726385
06 CITY # running:0.000103951s x0.938, miles:83.7957265568911
07 CITY # running:0.000172853s x1.663, miles:84.38275768767652
08 CITY # running:0.000295877s x1.712, miles:86.81329388311185
09 CITY # running:0.000194788s x0.658, miles:117.48644606825142
10 CITY # running:0.000561237s x2.881, miles:138.81613776560428
11 CITY # running:0.00122714s x2.186, miles:138.90486770025527
12 CITY # running:0.00112915s x0.920, miles:111.91943722100241
13 CITY # running:0.00251889s x2.231, miles:119.28734825523657
14 CITY # running:0.00112677s x0.447, miles:138.9351687014016
15 CITY # running:0.00363898s x3.230, miles:143.40710433454487
16 CITY # running:0.00422215s x1.160, miles:141.20115071627612
17 CITY # running:0.00317502s x0.752, miles:140.3956233158474
18 CITY # running:0.00864196s x2.722, miles:138.06138338625075
19 CITY # running:0.00527477s x0.610, miles:156.9575546092291
20 CITY # running:0.01158s x2.195, miles:158.180599617733
21 CITY # running:0.0158017s x1.365, miles:148.4486594113799
22 CITY # running:0.0177729s x1.125, miles:160.38397243365978
23 CITY # running:0.0214119s x1.205, miles:172.35758384201588
24 CITY # running:0.0219209s x1.024, miles:164.01914495590222
25 CITY # running:0.0298328s x1.361, miles:157.94880470955093
26 CITY # running:0.053242s x1.785, miles:175.89768884043787
27 CITY # running:0.0453973s x0.853, miles:171.76742774695765
28 CITY # running:0.0368412s x0.812, miles:164.7937952654588
29 CITY # running:0.0324101s x0.880, miles:173.53782962832412
30 CITY # running:0.0262458s x0.810, miles:172.3029374025116
31 CITY # running:0.061178s x2.331, miles:189.87633769587748
32 CITY # running:0.0482879s x0.789, miles:208.5764754571359
33 CITY # running:0.052141s x1.080, miles:202.12158656239455
[0, 15, 24, 32, 25, 20, 28, 27, 14, 5, 4, 31, 3, 29, 6, 7, 1, 9, 10, 11, 17, 2, 19, 
26, 8, 30, 22, 23, 21, 18, 16, 13, 12]

虽然并不是最优的解，但是速度非常快。用枚举法解全部的34个城市的最短路径，总共有 $33!/2$ 中情况，一共大约有 $4.34\times 10^{36}$ 中情况，这要迭代非常长的时间，而使用爬山法几乎是瞬间解决。并且在测试中也能看出，耗时时间随城市个数的增多并没有明显的变化！

局部束搜索解TSP问题

为了提高准确性，可以使用局部束搜索。

局部束搜索(local beam search)算法记录k个状态而不是只记录一个。它从k个随机生成的状态开始，每一步全部k个状态的所有后继全部被生成。如果其中有一个是目标状态，算法停止，否则从整个后继列表中选择k个最佳的后继，重复该过程：

from random import sample
from collections import namedtuple
from itertools import combinations
import math
import time
def local_beam_search(cities, best_n=5):
    class BeamNode:
        def __init__(self, miles, path, best):
            self.miles, self.path, self.best = miles, path, best
    def calc_miles(path):
        pre_pos = cities[path[-1]]
        tp_miles = 0
        for p in path:
            tp_miles += math.hypot(pre_pos[0]-cities[p][0],
                                  pre_pos[1]-cities[p][1])
            pre_pos = cities[p]
        return tp_miles
    beamnodes = [BeamNode(float('inf'),
        [0] + sample(range(1,len(cities)),len(cities)-1),
        False) for i in range(best_n)
    ]
    while True:
        if all(bn.best for bn in beamnodes):
            break
        origin_len = len(beamnodes)
        for bn in beamnodes[:best_n]:
            if bn.best:
                continue
            swap_poses = combinations(range(1, len(cities)), 2)
            bn.best = True
            for p1, p2 in swap_poses:
                tp_path = bn.path[:]
                tp_path[p1],tp_path[p2]=tp_path[p2],tp_path[p1]
                tp_miles = calc_miles(tp_path)
                if bn.miles>tp_miles:
                    beamnodes.append(BeamNode(tp_miles, tp_path, False))
                    bn.best = False
        for i in range(origin_len-1, -1, -1):
            if beamnodes[i].best==False:
                del beamnodes[i]
        beamnodes.sort(key=lambda b:b.miles)
        for i in range(len(beamnodes)-1,0,-1):
            if beamnodes[i].path==beamnodes[i-1].path:
                del beamnodes[i]
        del beamnodes[best_n:]
    return beamnodes[0].miles, beamnodes[0].path

pre_running = float('inf')
for i in range(1,len(cities)):
    t1 = time.time()
    miles2, path2 = local_beam_search(cities[:i])
    t2 = time.time()
    print("{:02} CITY # running:{:g}s x{:.3f}, miles:{}".format(
        i,t2-t1, (t2-t1)/pre_running, miles2))
    pre_running = t2-t1
    
print(path2)

结果为：

01 CITY # running:0.000131845s x0.000, miles:inf
02 CITY # running:8.39233e-05s x0.637, miles:inf
03 CITY # running:0.000100851s x1.202, miles:20.120564493919822
04 CITY # running:0.000149012s x1.478, miles:39.42664606580856
05 CITY # running:0.000249863s x1.677, miles:67.77227033726385
06 CITY # running:0.000396967s x1.589, miles:83.7957265568911
07 CITY # running:0.000697136s x1.756, miles:84.38275768767652
08 CITY # running:0.00139284s x1.998, miles:84.85443680089674
09 CITY # running:0.0025003s x1.795, miles:92.40225788702355
10 CITY # running:0.00446177s x1.784, miles:110.34594071307717
11 CITY # running:0.00586319s x1.314, miles:110.43467064772817
12 CITY # running:0.00724792s x1.236, miles:111.91943722100241
13 CITY # running:0.0120242s x1.659, miles:112.50512934569768
14 CITY # running:0.0183392s x1.525, miles:113.56609907838035
15 CITY # running:0.0246849s x1.346, miles:120.31428812090877
16 CITY # running:0.026643s x1.079, miles:125.13198234267095
17 CITY # running:0.0337448s x1.267, miles:137.43478593530628
18 CITY # running:0.0557592s x1.652, miles:127.2616818070425
19 CITY # running:0.0731211s x1.311, miles:136.19308169633763
20 CITY # running:0.106837s x1.461, miles:141.79488720470593
21 CITY # running:0.0689609s x0.645, miles:133.51852009103368
22 CITY # running:0.122045s x1.770, miles:146.1424850063973
23 CITY # running:0.122695s x1.005, miles:137.37416157720375
24 CITY # running:0.180004s x1.467, miles:153.8002244978345
25 CITY # running:0.213181s x1.184, miles:141.820048214232
26 CITY # running:0.235387s x1.104, miles:157.60764815422064
27 CITY # running:0.300357s x1.276, miles:151.5022530319789
28 CITY # running:0.316988s x1.055, miles:167.93297389468225
29 CITY # running:0.448021s x1.413, miles:160.47833032590472
30 CITY # running:0.388789s x0.868, miles:172.22641594558672
31 CITY # running:0.489542s x1.259, miles:166.34471516518593
32 CITY # running:0.528914s x1.080, miles:189.50448051112315
33 CITY # running:0.665572s x1.258, miles:187.31870592623517
[0, 1, 15, 2, 19, 17, 18, 23, 22, 27, 14, 5, 4, 31, 28, 13, 12, 11, 10, 9, 7, 6, 29, 
3, 30, 8, 26, 24, 32, 25, 20, 21, 16]

局部束搜索的时间复杂度也非常低。和爬山法一样，并不能保证路径最优，下面来计算一下 100 次 24城市路径规划，使用束搜索比首优爬山法更好的比例：

>>> sum(climb_TSP(cities)>=local_beam_search(cities) for i in range(100))
77
>>> sum(climb_TSP(cities[:15])>=local_beam_search(cities[:15]) for i in range(100))
89
>>> sum(climb_TSP(cities[:12])>=local_beam_search(cities[:12]) for i in range(100))
88
>>> sum(climb_TSP(cities[:8])>=local_beam_search(cities[:8]) for i in range(100))
96

可以看出，差不多有 80% 以上的概率是使用局部束搜索路径要小于等于首优爬山法。

遗传算法+局部束搜索解决TSP问题

在局部束搜索选出最优的若干个后继之后，再进行杂交，并选出其中的最优解决方案：

def genetic_lbs(cities, best_n=5):
    class BeamNode:
        def __init__(self, miles, path, best):
            self.miles, self.path, self.best = miles, path, best
    def calc_miles(path):
        pre_pos = cities[path[-1]]
        tp_miles = 0
        for p in path:
            tp_miles += math.hypot(pre_pos[0]-cities[p][0],
                                  pre_pos[1]-cities[p][1])
            pre_pos = cities[p]
        return tp_miles
    beamnodes = [BeamNode(float('inf'),
        [0] + sample(range(1,len(cities)),len(cities)-1),
        False) for i in range(best_n)
    ]
    while True:
        if all(bn.best for bn in beamnodes):
            break
        origin_len = len(beamnodes)
        for bn in beamnodes[:best_n]:
            if bn.best:
                continue
            swap_poses = combinations(range(1, len(cities)), 2)
            bn.best = True
            for p1, p2 in swap_poses:
                tp_path = bn.path[:]
                tp_path[p1],tp_path[p2]=tp_path[p2],tp_path[p1]
                tp_miles = calc_miles(tp_path)
                if bn.miles>tp_miles:
                    beamnodes.append(BeamNode(tp_miles, tp_path, False))
                    bn.best = False
        for i in range(origin_len-1, -1, -1):
            if beamnodes[i].best==False:
                del beamnodes[i]
        beamnodes.sort(key=lambda b:b.miles)
        for i in range(len(beamnodes)-1,0,-1):
            if beamnodes[i].path==beamnodes[i-1].path:
                del beamnodes[i]
        # 添加遗传算法部分
        cur_len = len(beamnodes)
        for i in range(cur_len):
            if i >= best_n:break
            for j in range(i+1, cur_len):
                if i+j>=best_n:break
                for k in range(best_n-i-j):
                    # 基因交叉
                    cut_pos = int(random.uniform(0,1)*len(cities))
                    gene1 = beamnodes[i].path[:cut_pos]
                    for c in beamnodes[j].path:
                        if c not in gene1:
                            gene1.append(c)
                    gene2 = beamnodes[j].path[:cut_pos]
                    for c in beamnodes[i].path:
                        if c not in gene2:
                            gene2.append(c)
                    for gn in (gene1, gene2):
                        beamnodes.append(BeamNode(calc_miles(gn), gn, False))
        beamnodes.sort(key=lambda b:b.miles)
        del beamnodes[best_n:]
    return beamnodes[0].miles, beamnodes[0].path

pre_running = float('inf')
for i in range(1,len(cities)):
    t1 = time.time()
    miles2, path3 = genetic_lbs(cities[:i])
    t2 = time.time()
    print("{:02} CITY # running:{:g}s x{:.3f}, miles:{}".format(
        i,t2-t1, (t2-t1)/pre_running, miles2))
    pre_running = t2-t1
    
print(path3)

结果为：

01 CITY # running:7.70092e-05s x0.000, miles:inf
02 CITY # running:7.72476e-05s x1.003, miles:inf
03 CITY # running:0.000236034s x3.056, miles:20.120564493919822
04 CITY # running:0.000288963s x1.224, miles:39.42664606580856
05 CITY # running:0.000902891s x3.125, miles:67.77227033726385
06 CITY # running:0.000638008s x0.707, miles:83.7957265568911
07 CITY # running:0.00062108s x0.973, miles:86.09074760487061
08 CITY # running:0.000916004s x1.475, miles:93.99538523941173
09 CITY # running:0.00176096s x1.922, miles:94.36111496923868
10 CITY # running:0.00226212s x1.285, miles:119.48688915159217
11 CITY # running:0.00388813s x1.719, miles:111.54364423814188
12 CITY # running:0.00667977s x1.718, miles:110.68732069001533
13 CITY # running:0.010855s x1.625, miles:139.12310427782793
14 CITY # running:0.00950813s x0.876, miles:126.04272022825214
15 CITY # running:0.028379s x2.985, miles:120.44915681149206
16 CITY # running:0.0164061s x0.578, miles:132.938090495729
17 CITY # running:0.04386s x2.673, miles:128.48588951678107
18 CITY # running:0.0216119s x0.493, miles:136.65881442937123
19 CITY # running:0.0252399s x1.168, miles:154.52207364775006
20 CITY # running:0.044533s x1.764, miles:139.24244007981014
21 CITY # running:0.0570438s x1.281, miles:130.2661038148359
22 CITY # running:0.0877109s x1.538, miles:131.81266129344394
23 CITY # running:0.163138s x1.860, miles:152.9714314175534
24 CITY # running:0.105285s x0.645, miles:139.87220750546572
25 CITY # running:0.117091s x1.112, miles:137.70206639387885
26 CITY # running:0.144975s x1.238, miles:147.58883108921282
27 CITY # running:0.189689s x1.308, miles:158.66268651198612
28 CITY # running:0.241267s x1.272, miles:152.15471407050538
29 CITY # running:0.274257s x1.137, miles:170.46777589913202
30 CITY # running:0.211076s x0.770, miles:191.00544805184
31 CITY # running:0.306311s x1.451, miles:160.18260092406962
32 CITY # running:0.292734s x0.956, miles:190.20971445669596
33 CITY # running:0.483113s x1.650, miles:185.0191452526489
[0, 23, 21, 20, 25, 11, 10, 9, 7, 28, 3, 29, 6, 27, 14, 5, 4, 31, 30, 8, 26, 32, 24, 
22, 16, 13, 12, 18, 17, 19, 2, 15, 1]

下面再测试一下解决方案的效果是否得到提高：

>>> sum(local_beam_search(cities)>=genetic_lbs(cities) for i in range(100))
52
>>> sum(local_beam_search(cities[:15])>=genetic_lbs(cities[:15]) for i in range(100))
33
>>> sum(local_beam_search(cities[:12])>=genetic_lbs(cities[:12]) for i in range(100))
33
>>> sum(local_beam_search(cities[:8])>=genetic_lbs(cities[:8]) for i in range(100))
39

在这个实例中，添加了遗传算法之后，结果居然变差了。但是，并不是说遗传算法不行，而是遗传算法不适合这个问题。

总结

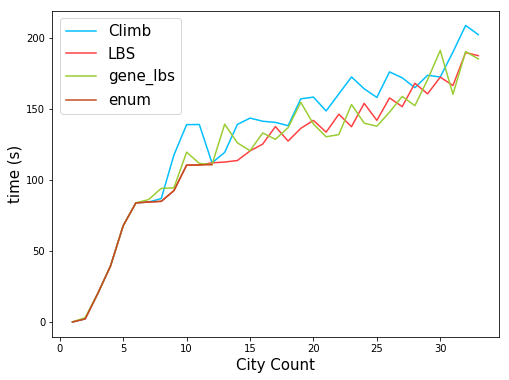
T : 求解时间(s) ，Path : 路径长度

时间性能对比表

城市个数	枚举	爬山法	局部束	遗传局部束
01	0.000036	0.000021	0.000132	0.000077
02	0.000011	0.000018	0.000084	0.000077
03	0.000009	0.001722	0.000101	0.000236
04	0.000022	0.000065	0.000149	0.000289
05	0.000049	0.000111	0.000250	0.000903
06	0.000366	0.000104	0.000397	0.000638
07	0.002003	0.000173	0.000697	0.000621
08	0.018006	0.000296	0.001393	0.000916
09	0.145260	0.000195	0.002500	0.001761
10	1.162350	0.000561	0.004462	0.002262
11	12.708600	0.001227	0.005863	0.003888
12	148.912000	0.001129	0.007248	0.006680
13	-	0.002519	0.012024	0.010855
14	-	0.001127	0.018339	0.009508
15	-	0.003639	0.024685	0.028379
16	-	0.004222	0.026643	0.016406
17	-	0.003175	0.033745	0.043860
18	-	0.008642	0.055759	0.021612
19	-	0.005275	0.073121	0.025240
20	-	0.011580	0.106837	0.044533
21	-	0.015802	0.068961	0.057044
22	-	0.017773	0.122045	0.087711
23	-	0.021412	0.122695	0.163138
24	-	0.021921	0.180004	0.105285
25	-	0.029833	0.213181	0.117091
26	-	0.053242	0.235387	0.144975
27	-	0.045397	0.300357	0.189689
28	-	0.036841	0.316988	0.241267
29	-	0.032410	0.448021	0.274257
30	-	0.026246	0.388789	0.211076
31	-	0.061178	0.489542	0.306311
32	-	0.048288	0.528914	0.292734
33	-	0.052141	0.665572	0.483113

曲线图为：

由于枚举法的时间复杂度实在太大，故没有在图中画出来。

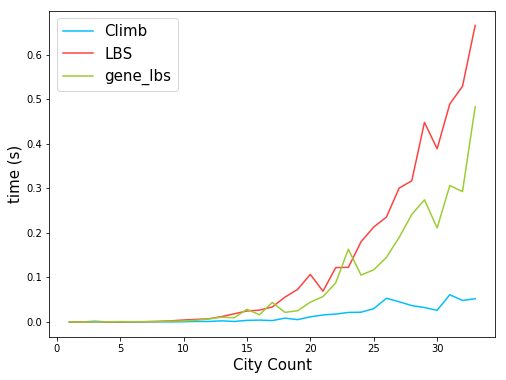
结果对比表

城市个数	枚举	爬山法	局部束	遗传局部束
01	0.00	0.00	0.00	0.00
02	2.16	2.17	2.17	3.00
03	20.12	20.12	20.12	20.12
04	39.43	39.43	39.43	39.43
05	67.77	67.77	67.77	67.77
06	83.80	83.80	83.80	83.80
07	84.38	84.38	84.38	86.09
08	84.85	86.81	84.85	94.00
09	92.40	117.49	92.40	94.36
10	110.35	138.82	110.35	119.49
11	110.43	138.90	110.43	111.54
12	110.69	111.92	111.92	110.69
13	-	119.29	112.51	139.12
14	-	138.94	113.57	126.04
15	-	143.41	120.31	120.45
16	-	141.20	125.13	132.94
17	-	140.40	137.43	128.49
18	-	138.06	127.26	136.66
19	-	156.96	136.19	154.52
20	-	158.18	141.79	139.24
21	-	148.45	133.52	130.27
22	-	160.38	146.14	131.81
23	-	172.36	137.37	152.97
24	-	164.02	153.80	139.87
25	-	157.95	141.82	137.70
26	-	175.90	157.61	147.59
27	-	171.77	151.50	158.66
28	-	164.79	167.93	152.15
29	-	173.54	160.48	170.47
30	-	172.30	172.23	191.01
31	-	189.88	166.34	160.18
32	-	208.58	189.50	190.21
33	-	202.12	187.32	185.02

曲线图为：