函数拟合--正规方程

正规方程：
$\bold w=(\bold X^{(train)T}\bold X^{(train)})^{-1}\bold X^{(train)T}\bold y^{(train)}$
也可以简写为：
$\bold w=(\bold X\bold X^T)^{-1}\bold X^T\bold y$

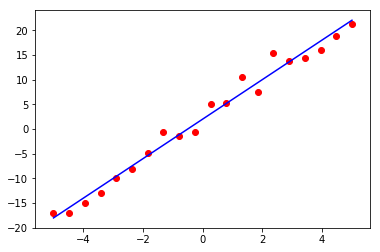
实验：正规方程拟合一次函数

import matplotlib.pyplot as plt
import numpy as np
def f(x):
    return x*3.861+1.552

X = np.hstack((np.linspace(-5,5,20).reshape(-1,1),np.ones((20,1))*1))

y = f(X[:,0]).reshape(-1,1)+np.random.randn(20,1)*2

# 用公式求权重
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
print(list(w))
hat_y = X.dot(w)
plt.plot(X[:, 0], hat_y, c='b')
plt.scatter(X[:,0],y[:,0], c='r')
plt.show()

得到的 w 为 : [4.00654227, 2.03617416]

绘制的图像为：

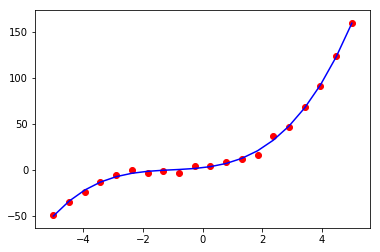
实验：正规方程拟合高次函数

import matplotlib.pyplot as plt
import numpy as np
def f(x):
    return x*3.861+2.12*x**2+0.67*x**3+1.552

X = np.hstack((np.linspace(-5,5,20).reshape(-1,1),np.ones((20,1))*1))
# 拟合最高次为4的函数
X = np.hstack((X[:,0].reshape(-1,1),
               (X[:,0]**2).reshape(-1,1),
               (X[:,0]**3).reshape(-1,1),
               (X[:,0]**4).reshape(-1,1),
               X[:,-1].reshape(-1,1)))

y = f(X[:,0]).reshape(-1,1)+np.random.randn(20,1)*2

# 用公式求权重
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
print(list(w.flatten()))
hat_y = X.dot(w)
plt.plot(X[:, 0], hat_y, c='b')
plt.scatter(X[:,0],y[:,0], c='r')
plt.show()

代码和一次函数的拟合非常相似，不同在于特征加入了高次，得到的 w 为：[3.71743889404003, 2.1291721826267382, 0.68793620217190288, -0.0017444665565614081, 2.2658935002908454]。由于在真实的 $f$ 中并没有4次项，故4次项特征对应的权重为-0.0017444665565614081，远小于其他权重。

绘制的图像为：

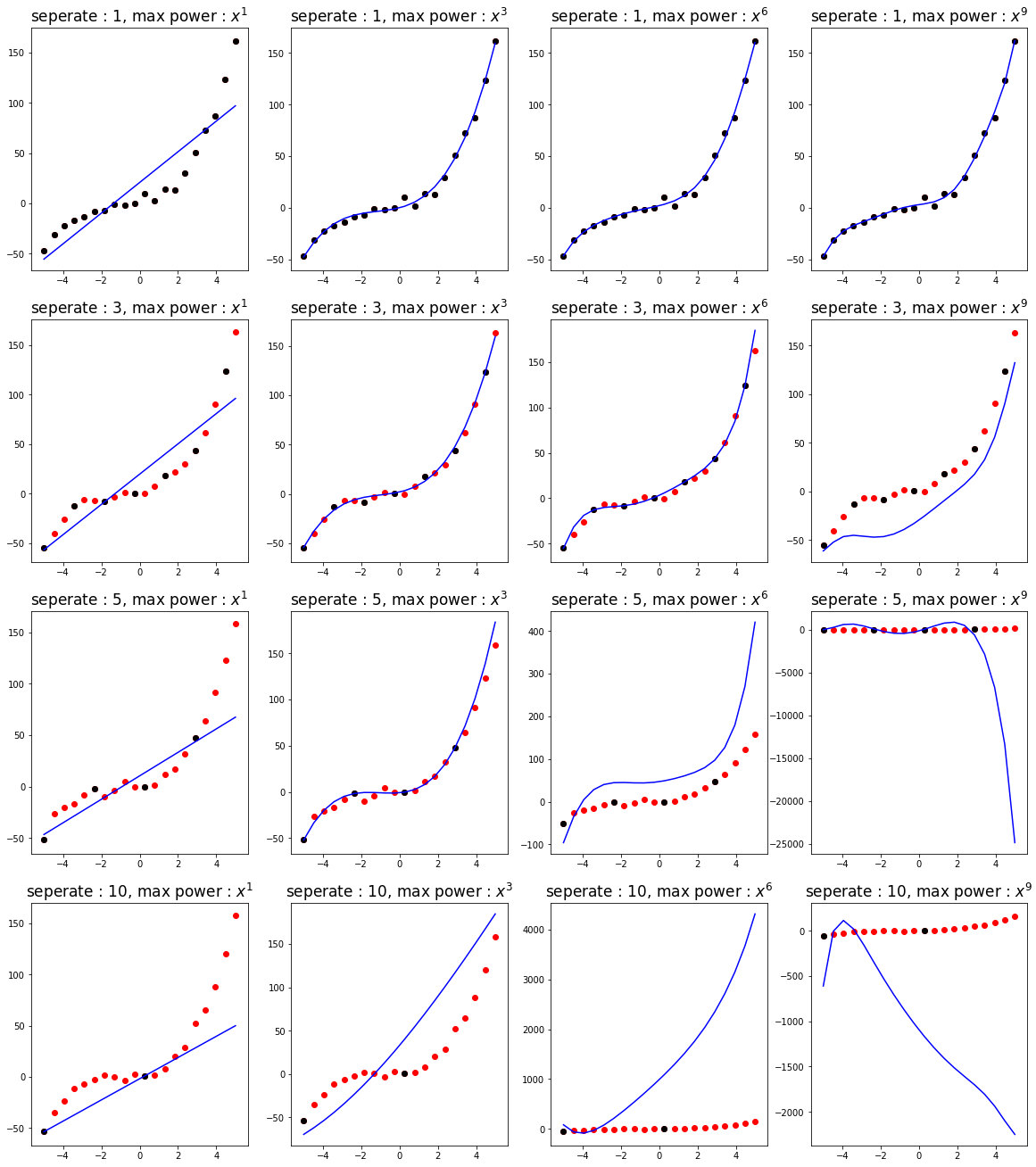
实验：采样点个数对正规方程拟合的影响

本实验主要探究不同的采样点多少对不同次的模型的影响：

import matplotlib.pyplot as plt
import numpy as np
import random
def f(x):
    return x*3.861+2.12*x**2+0.67*x**3+1.552
# 通过采样间隔控制采样点的个数
def test(seperate):
    X = np.hstack((np.ones((20,1)), np.linspace(-5,5,20).reshape(-1,1)))

    X = np.hstack((X[:,0].reshape(-1,1),
                   X[:,1].reshape(-1,1),
                   (X[:,1]**2).reshape(-1,1),
                   (X[:,1]**3).reshape(-1,1),
                   (X[:,1]**4).reshape(-1,1),
                   (X[:,1]**5).reshape(-1,1),
                   (X[:,1]**6).reshape(-1,1),
                   (X[:,1]**7).reshape(-1,1),
                   (X[:,1]**8).reshape(-1,1),
                   (X[:,1]**9).reshape(-1,1)
                  ))
    y = f(X[:,1]).reshape(-1,1)+np.random.randn(len(X),1)*3
    # 抽取若干样本点
    selected = list(range(0,20,seperate))
    # 抽取 0~1 次作为特征
    X_1 = X[selected][:,:2]
    # 抽取 0~3 次作为特征
    X_3 = X[selected][:,:4]
    # 抽取 0~6 次作为特征
    X_6 = X[selected][:,:7]
    # 抽取 0~9 次作为特征
    X_9 = X[selected][:,:10]
    
    plt.figure(figsize=(20,5))
    for i,X_i in enumerate((X_1, X_3, X_6, X_9)):
        w = np.linalg.inv(X_i.T.dot(X_i)).dot(X_i.T).dot(y[selected])
        hat_y = X[:, :len(w)].dot(w)
        plt.subplot(1,4,i+1)
        plt.title(f"seperate : {seperate}, max power : $x^{len(w)-1}$", fontsize=17)
        plt.plot(X[:, 1], hat_y[:, 0], c='b')
        plt.scatter(X[:,1],y[:,0], c='r')
        plt.scatter(X[selected,1],y[selected,0], c='k')
    plt.show()
# 采样间隔为1，不丢失采样点
test(1)
# 采样间隔为3，丢失2/3的采样点
test(3)
# 采样间隔为5，丢失4/5的采样点
test(5)
# 采样间隔为10，丢失9/10的采样点
test(10)

实验 : 正规方程+正则化

我们希望通过正规化，让机器能够自动选择最高次数，我们通过实验看看 $\lambda$ 对训练的影响：

import matplotlib.pyplot as plt
import numpy as np
import random

def f(x):
    return x*3.861+2.12*x**2+0.67*x**3+1.552

def MSE(hat_y, y):
    return (sum((hat_y-y)**2)/len(y)).flatten()[0]

X = np.hstack((np.ones((20,1)), np.linspace(-5,5,20).reshape(-1,1)))

X = np.hstack((X[:,0].reshape(-1,1),
               X[:,1].reshape(-1,1),
               (X[:,1]**2).reshape(-1,1),
               (X[:,1]**3).reshape(-1,1),
               (X[:,1]**4).reshape(-1,1),
               (X[:,1]**5).reshape(-1,1),
               (X[:,1]**6).reshape(-1,1),
               (X[:,1]**7).reshape(-1,1),
               (X[:,1]**8).reshape(-1,1),
               (X[:,1]**9).reshape(-1,1)
              ))
# 固定随机化过程，阅读代码时这句可忽略
np.random.seed(6666)
y = f(X[:,1]).reshape(-1,1)+np.random.randn(len(X),1)*8
# 抽取若干样本点
selected = list(range(0,20,3))

plt.figure(figsize=(20,5))
lamds = (0,5,10,20)
# 遍历 λ 的值
for f_n,lamd in enumerate(lamds):
    b_cost = b_hat_y = b_power = None
    for i in range(X.shape[1]):
        X_i = X[selected][:, :(i+1)]
        w = np.linalg.inv(X_i.T.dot(X_i)).dot(X_i.T).dot(y[selected])
        hat_y = X[:, :len(w)].dot(w)
        # 计算带正则化项的损失
        cur_cost = MSE(hat_y[selected,:], y[selected,:]) + i*lamd
        if b_cost==None or b_cost>cur_cost:
            b_cost = cur_cost
            b_hat_y = hat_y
            b_power = i
    plt.subplot(1,len(lamds), f_n+1)
    plt.title(f"$\lambda$: {lamd};max power: $x^{b_power}$", fontsize=17)
    plt.plot(X[:, 1], b_hat_y[:, 0], c='b')
    plt.scatter(X[:,1],y[:,0], c='r')
    plt.scatter(X[selected,1],y[selected,0], c='k')
    plt.ylim(-60, 170)
plt.show()

最后的结果为：

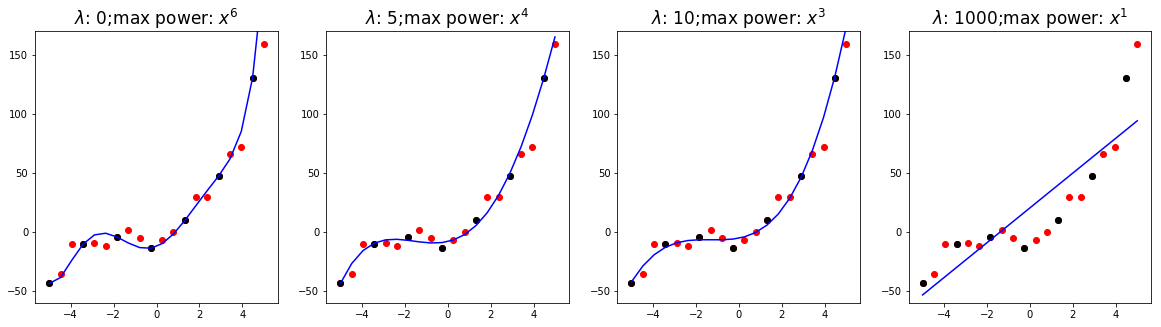
其中黑色的点是提供给机器进行学习的样本点，红色的点是全部的样本点。

我们所提供的正则化项偏向于选择最高次系数较小的模型。可以看出，在 $\lambda=0$ （即没有正则化）时，选择了最高次为 6 的模型，并且该模型也通过了所有的黑点。而随着 $\lambda$ 的增大，选择的最高次也越来越小。当选择的 $\lambda$ 过大时，模型变为简单的 1 次。