启发式函数——8数码问题

八数码问题也称为九宫问题。在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。

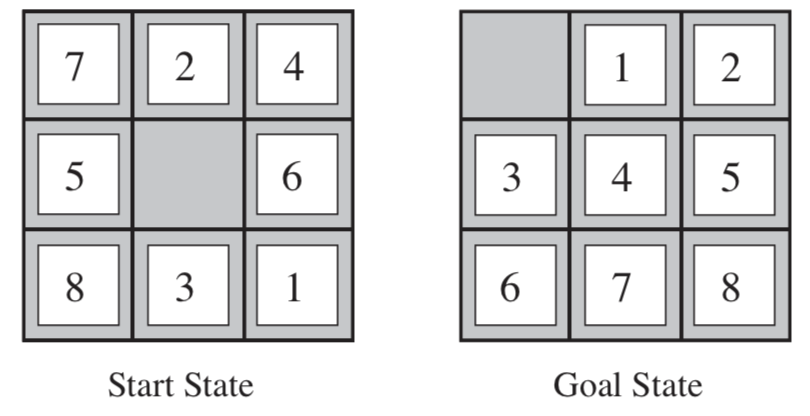
8 dight

一个随机产生的八数码问题的平均解步数为22。

问题建模

构建 8 数码问题的模型为：

import copy
class EightDight:
    opt = {'U':(-1,0), 'D':(1,0),'L':(0,-1), 'R':(0,1)}
    def __init__(self, init_state, final_state=None):
        if final_state == None:
            final_state = [[0,1,2],
                          [3,4,5],
                          [6,7,8]]
        self.final = final_state
        self.state = copy.deepcopy(init_state)
    @property
    def state(self):
        return self._state
    @state.setter
    def state(self, state):
        self._state = copy.deepcopy(state)
        for i in range(3):
            for j in range(3):
                if self.state[i][j]==0:
                    self.zero_pos = (i, j)
        return
    def judge_opt(self, opt):
        """Judge opt is valid or not
        """
        future_pos = (self.zero_pos[0]+self.opt[opt][0],
                     self.zero_pos[1]+self.opt[opt][1])
        return all(0<=i<3 for i in future_pos)
    
    def get_valid_opts(self):
        return [o for o in self.opt if self.judge_opt(o)]
    
    def operator(self, opts):
        for opt in opts:
            opt = str.upper(opt)
            if self.judge_opt(opt)==False:
                return
            p_f = (self.zero_pos[0]+self.opt[opt][0],
                   self.zero_pos[1]+self.opt[opt][1])
            p_z = self.zero_pos
            self.state[p_z[0]][p_z[1]]=self.state[p_f[0]][p_f[1]]
            self.state[p_f[0]][p_f[1]]=0
            self.zero_pos = p_f
        
    def __str__(self):
        s = []
        for i in self.state:
            s.append(' '.join(str(n) for n in i))
        return '\n'.join(s)+'\n'

    def __iter__(self):
        for i in self.state:
            yield tuple(i)
    

init_state = [[7,2,4],[5,0,6],[8,3,1]]
e = EightDight(init_state)
print(e)
print(e.get_valid_opts(), '\n')
e.operator('U')
print(e)

测试结果：

7 2 4
5 0 6
8 3 1

['U', 'D', 'L', 'R'] 

7 0 4
5 2 6
8 3 1

BFS-1

不记录重复状态，为了节省内存空间，程序记录的是操作步骤而不是状态。因此，每次为了得到某个状态，必须用记录的步骤执行操作过程。代码如下：

def BFS_1(init_state):
    """
    记录的是操作步骤，每次迭代时需要重新计算当前状态
    """
    from collections import deque
    e = EightDight(init_state)
    frontier = deque([""])
    while True:
        cur_opts = frontier.popleft()
        e.state = init_state
        e.operator(cur_opts)
        if e.state==e.final:
            break
        for sub_opt in e.get_valid_opts():
            frontier.append(cur_opts+sub_opt)
    return cur_opts

进过测试，该代码非常费时，而且在操作序列很长时，空间也并没有减少多少。关键是没有记录重复状态，因此该搜索是树搜索而非图搜索，这也是费时的最大原因。

BFS-2

记录状态，使得树搜索变为图搜索，大大又花了时间复杂度和空间复杂度：

def BFS_2(init_state):
    """
    记录的是操作步骤，每次迭代时需要重新计算当前状态
    """
    from collections import deque
    e = EightDight(init_state)
    frontier = deque([""])
    explored = set([tuple(e)])
    best_actions = None
    while best_actions==None and len(frontier):
        cur_opts = frontier.popleft()
        e.state = init_state
        e.operator(cur_opts)
        if e.state==e.final:
            best_actions = cur_opts
            break
        cur_state = e.state
        for sub_opt in e.get_valid_opts():
            e.state = cur_state
            e.operator(sub_opt)
            if e.final==e.state:
                best_actions = cur_opts + sub_opt
                break
            if tuple(e) not in explored:
                explored.add(tuple(e))
                frontier.append(cur_opts+sub_opt)
    return best_actions

init_state = [[7,2,4],[5,0,6],[8,3,1]]
BFS_2(init_state)

求得的结果为：'LURDDLURRULLDRRDLURULDDLUU'
所用时间为：

CPU times: user 16.5 s, sys: 68.8 ms, total: 16.5 s
Wall time: 16.6 s

A* 算法 / 贪婪算法

A*、贪婪算法其实和BFS、DFS、Uniform Cost Search算法都类似，就是对 frontier 数组的排序不同：

frontier 使用队列，即FIFO，即为BFS
frontier 使用堆栈，即FILO，即为DFS
frontier 使用统一的代价估计，并最先弹出其中最小的代价状态，即为UCS
frontier 的排序自定义，使用启发式函数 f = g + h，其中 g 表示到当前状态所用的“距离”，h 表示估计到目标的距离，为了找到最优解，h 需要满足可采纳性和一致性
- g 取实际所用距离，h = (到达目标状态?)0:1：变形为为BFS
- g ≡ 0，h 满足一致性和可采纳性：贪婪算法
- g 取实际使用距离，h 满足一致性和可采纳性：A* 算法
- g ≡ 0，h = (到达目标状态?)0:1：变形为DFS/BFS（根据f相等时，前插入则为DFS，后插入则为BFS）

可见 BFS 为 A* 的一种特殊情况而已。

下面为 8数字问题对应的 A* 的算法：

def heuristic_framework(init_state, heuristic):    
    from collections import namedtuple, deque
    Record = namedtuple('Record', 'actions h_cost')
    e = EightDight(init_state)
    frontier = deque([Record('', e.heuristic_cost(heuristic))])
    best_actions =None
    explored = set([tuple(e)])
    while len(frontier) and best_actions==None:
        cur_opts = frontier.popleft()
        if cur_opts.h_cost==0:
            best_actions = cur_opts.actions
            break
        e.state = init_state
        e.operator(cur_opts.actions)
        tp_state = e.state
        for opt in e.get_valid_opts():
            e.state = tp_state
            e.operator(opt)
            if tuple(e) in explored:
                continue
            explored.add(tuple(e))
            h_cost = e.heuristic_cost(heuristic)
            tp_record = Record(cur_opts.actions+opt, h_cost)
            # 下面3行注释掉是为了保证最优性，否则效率可能会提高
            # 但是并不能保证最优性
            # if h_cost==0:
            #     best_actions = tp_record.actions
            #     break
            cur_f = len(tp_record.actions)+tp_record.h_cost
            left,right = 0, len(frontier)-1
            # 使用二分查找，大大加快查询插入位置的速度
            while left<=right:
                mid = (left+right)//2
                if len(frontier[mid].actions)+frontier[mid].h_cost < cur_f:
                    left = mid+1
                else:
                    right = mid-1
            frontier.insert(left, tp_record)
    return best_actions

该函数需要传入一个启发式函数。

类 BFS 的启发式函数

启发式函数为 h = (到达目标状态?)0:1：

def heuristic_arrive(cur_state, final_state):
    return int(not cur_state==final_state)

%time heuristic_framework(init_state, heuristic_arrive)

结果为：

CPU times: user 19 s, sys: 94 ms, total: 19.1 s
Wall time: 19.1 s
[out] : 'LURDRDLLURRDLLURRULLDRRULL'

A* 变形的 BFS 比真实的BFS要稍稍慢一点，因为需要寻找插入位置，结果满足最优性。

数字不正确的个数作启发式函数

def heuristic_diff(cur_state, final_state):
    """
    使用棋子不在其位的个数作为启发式函数
    """
    h_cost = 0
    for r1, r2 in zip(cur_state, final_state):
        for c1, c2 in zip(r1, r2):
            h_cost += int(c1!=c2)
    return h_cost

%time heuristic_framework(init_state, heuristic_diff)

结果为：

CPU times: user 4.13 s, sys: 8.13 ms, total: 4.14 s
Wall time: 4.15 s
[out] : 'LURDDLURRULLDRRDLURULDDLUU'

可以发现，比BFS快了3倍，效果非常不错。结果满足最优性。

曼哈顿距离作为启发式函数

def heuristic_Manhattan(cur_state, final_state):
    """
    使用棋子的曼哈顿距离作为启发式函数
    """
    cur_pos = [0]*9
    final_pos = [0]*9
    for i in range(3):
        for j in range(3):
            cur_pos[cur_state[i][j]] = (i, j)
            final_pos[final_state[i][j]] = (i, j)
    h_cost = 0
    for p1, p2 in zip(cur_pos, final_pos):
        h_cost += abs(p1[0]-p2[0])+abs(p1[1]-p2[1])
    return h_cost

%time heuristic_framework(init_state, heuristic_Manhattan)

结果为：

CPU times: user 351 ms, sys: 3.44 ms, total: 354 ms
Wall time: 364 ms
[out] : 'LURDRDLLURRDLLURRULLDRRULL'

只花了半秒钟不到，性能与BFS相比整整提高了40多倍，与使用不正确的数字作为启发式函数相比提高了13倍！并且结果满足最优性。

可见选择合适的启发式函数对于寻找问题的解影响非常大。

使用 heuristic_diff 和 heuristic_Manhattan 分析

从实际效果上可，heuristic_Manhanttan （后面记为 $h_1$ ）的速度比 heuristic_diff（后面记为 $h_2$ ）的速度快很多。从这两个启发式的定义很容易看出，对于任意结点 n， $h_1$ ≤ $h_2$ ，因此后一种启发式函数更有优势。优势可以直接转换为效率:使用 $h_2$ 的 A*算法永远不会比使用 $h_1$ 的A*算法扩展出更多的节点。

一般来说，使用值更大的启发式函数是好的，前提是计算该启发式花费的时间不是太多。

$h_1$ 假设每个棋子可以随便移动所求的 cost， $h_2$ 假设一个棋子可以向容易方向移动一步，甚至可以移动到被其他棋子占据的位置上。这些减少了行动限制的问题称为松弛问题，松弛问题的状态空间图是原来状态空间中的超图，原因是减少了限制导致图中边的增加。

如何通过计算机求出合理的启发式函数

那能否可以利用计算机自动生成高效的启发式函数呢？

一个名为 ABSOLVER 的程序可以从原问题的定义出发，使用“松弛问题”技术和各种其他技术自动地生成启发式。ABSOLVER 为 8 数码游戏找到了比以前已有的启发式都好的新启发式，并且为著名的魔方游戏找到了第一个有用的启发式。

生成新的启发式函数的难点在于经常不能找到“无疑最好的”启发式。如果可采纳启发式的集合 $h_1\cdots h_m$ 对问题是有效的，并且其中没有哪个比其他的更有优势，那我们应该如何选择？其实我们不用选择。我们可以这样定义新的启发式从而得到其中最好的： $h(n)=max \{ h_1(n),\cdots,h_m(n) \}$
这个合成的启发式使用的是对应于问题中节点的更精确的函数。因为它的每个成员启发式都是可采纳的，所以 $h$ 也是可采纳的，也很容易证明 $h$ 是一致的。此外， $h$ 比其他所有成员启发式更有优势。